greedy algs 和 local search algs 都通过做一系列最优化某些 local choice 的决策进行工作:
- greedy algs 属于 primal infeasible algs: 过程中构造一个 feasible solution
- local search algs 属于 primal feasible algs: 维护一个 feasible solution, 过程中不断修改它
Scheduling job with deadlines on a single machine
先考虑最简单的版本:
个 jobs 需要在一个机器上调度, 同一时间只能处理一个 job, 第 个 job 的 release date 为 , 需要的处理时间为 , 假定每个 job 还有一个 due date , 若我们在 时完成这个 job, 那么它的 lateness .
目标是最小化 .
这个问题是 NP-hard 的, 决定是否存在一个 schedule 使得 也是 strongly NP-hard 的, 很难得到 near-optimal solutions. 假设存在一个 -approximation algorithm, 那么对于所有最优解为 0 的输入, 它的解不会超过 , 这就会得出 的结论. 事先假定 是一个规避上述问题 easy workaround, 此时保证有 , 利用优先处理 due date 最小的 job 的 greedy heuristic 便可得到一个 2-approximation algorithm.
令 为 jobs 的某个子集, , 为 optimal value.
Lemma 2.1
For each subset of jobs,
考虑 中 最大的 job , 显然有 . 根据定义有, , 当机器处理 中的 jobs 没有任何闲置时有 , 存在闲置时有 , 因此有 . 于是
lemma 2.1 是对最优解极端情况的一个分析, 可以用来比较最优解与算法解的大小关系.
若 job 的 release date 就称它在 time 是 available 的. earliest due date (EDD) rule 指的是每当机器处于闲置时, 就处理下一个 due date 最早的 available job.
Theorem 2.2
The EDD rule is a 2-approximation algorithm for the problem of minimizing the maximum lateness on a single machine subject to release dates with negative due dates.
考虑算法得到的最大 lateness 对应的 job , 即 . 找到 之前的最小的 满足 的时间段机器没有任何闲置, 令 为这个时间段内 available jobs 的集合.
job 开始处理的时间为 , 在 时间段内机器没有闲置, 所以 , 所以 在 中至少有一段时间为 available job, 根据 的定义有 .
显然我们有 , 根据 lemma 2.1 有 . 将 代入 lemma 2.1 得到 与 的关系式: . 最后将两个不等式相加有
The -center problem
将大量 data 根据 similarities 和 dissimilarities 分类是现实世界中很普遍的需求, 这通常被称为 clustering data.
这里考虑 clustering 的一个变种, 即 -center problem:
给定一个无向完全图 , 中任意两点 之间的 distance 并约定 , 且遵循 triangle inequality: 任给三元组 , 有 . 在本题中, similarity 由 distance 决定: 越相近的点越相似. 给定 input , 要求找到 clusters 使得最相似的 vertices 处于同一 cluster 中.
问题等同于找出 为 个 cluster centers 的集合, 对每个点 , 定义 , 将其放入距离最近的 center 所处的 cluster 中, 目标是最小化 .
一个 simple & intuitive 的 greedy algorithm 是: 先随机将一个点加入 , 然后迭代 次, 每次在 中选取 最大的点 将其加入 .

Theorem 2.3
Algorithm 2.1 is a 2-approximation algorithm for the -center problem.
Proof
TODO
这个 approximation 是可能的最优值, 考虑 NP-complete 问题 dominating set problem:
给定 graph 和整数 , 需要 decide 是否存在大小为 的集合 使得每个结点要么在 中要么与 中的结点相邻.
给定一个 dominating set problem 的实例 , 构造一个 -center problem 实例 , 令 , 若 , 则令 , 否则令 . 此时 -center problem 所有可行解的值要么是 1 要么是 2, 若为 1, 则说明 dominating set problem 的答案为 true, 否则为 false. 假设我们有一个 -approximation algorithm for -center problem, 其中 , 那么只要最优解为 , 那么它至多返回 , 于是可以由算法的返回值来 decide, 这表明了以下定理.
Theorem 2.4
There is no -approximation algorithm for the -center problem for unless .
Scheduling jobs on identical parallel machines
个相同的 machine, 个 jobs 待处理, 每个 job 需要处理时间 , 不存在 release date 和 due date, 都在 时 release, 设完成时间为 , 目标是最小化 , 也将 称为 schedule 的 makespan 或 length.
可以将这个问题看作等价的 load-balancing problem:
个物品, 每个有一个 weight , 将其分配到 个 machine 上, 目标是最小化单个 machine 的 total weight.
即便是最简单的算法也能在这个 scheduling problem 的模型上取得 reasonably good 的结果.
利用 local search 来解决的一个算法是: 从任意 schedule 开始, 将当前 schedule 下最晚完成的 job 记作 , 检查是否存在一个 machine 使得将 分配给它能减小 即减小 makespan, 若存在则重新分配 , 否则 terminate. 不断重复上述过程直到 terminate.
job 在 reassign 前的开始时间为 , 若它能被 reassign 则表明存在 machine 的结束工作时间早于 . 在分析这个算法前先对 optimal solution 建立估计式. 由于每个 job 都要被处理, 肯定有
另外, 若每个 job 可以被 fractionally processed, 那么最优解必然是 , 于是有
考虑上述 local search algorithm 的解. 设 为最终 schedule 中最晚完成的 job, 即得到的解 , 它开始处理的时间为 , 由于 不能被 reassign, 所以在 这段时间内所有 machine 都没有空闲且这段时间至少还有一个 job 没有结束处理, 可以得到不等式
又有 , 于是
Theorem 2.5
The local search procedure for scheduling jobs on identical parallel machines is a 2-approximation algorithm.
不难发现简单修改一下不等式 2.5 可以进一步精确上述 approximation ratio:
继而
另一个 natural algorithm 是遍历 job 每次将 job 分配给当前最早完工的 machine 的 greedy algorithm, 这个算法被称为 list scheduling algorithm, 即可以将其看作为先将 jobs 按顺序排列为一个 list, 然后下一个被处理的 job 就是 list 中最上方的 job.
要分析这个 greedy algorithm, 不妨将它得到的 schedule 作为 local search algorithm 的初始 schedule, 此时 必然小于等于其他 machine 的结束时间, 于是 local search algorithm 会直接 terminate, 因此有以下定理.
Theorem 2.6
The list scheduling algorithm for the problem of minimizing the makespan on identical parallel machines is a 2-approximation algorithm.
显然 较大的 job 分配错误的惩罚也较大, 那么不妨在刚开始每个 machine 工作量相差不大时将 较大的 job 分配好, 后面 较小的再进行分配容错率就会高一些. 利用这个 heuristic 优化 list scheduling algorithm 即先将 job 按 从大到小排序之后再运行 list scheduling algorithm 便得到了一个新的算法, 它也被称为 longest processing time rule (LPT).
Theorem 2.7
The longest processing time rule is a -approximation algorithm for scheduling jobs to minimize the makespan on identical parallel machines.
考虑反证法。假设 LPT 的 approximation , 尝试找出反例使得 .
令 ,首先简化问题,不妨只考虑最晚完成的 job 是 最小的 job, 我们需要证明这个情况是存在的。不妨设 job 是最晚完成的 job 并且 ,那么直接丢掉第 个 job,算法的解不变,而最优解只会减小,于是我们可以得到一个满足要求的更小的反例,于是待证情况可以存在。
不妨记最晚完成的 job 为 , 显然 . 不难发现,在上述情况下,除非 , 否则必然有 , 即 前面一定有 job 和它在同一个机器上处理。类似于前面的证明,此处也有 , 不妨设 前面有 个 job 与它在同一机器上处理,那么有 , 若 , 这显然会有 , 不是个反例,于是我们需要找到 的情况。
在满足前面所述条件下, 所在机器共处理 个 job、其余机器每个都处理 个 job 的情况是 最小且 不会变的情况,我们考虑这样的极端情况。此时有 . 当 时,这个式子恒成立;当 时,;当 时,这要求 , 与前提条件矛盾,反例不存在。
最后, 的情况比较简单,此时 LPT 的解必然就是最优解,同样不存在反例。具体而言,当 时,显然将 给前面最早结束的机器处理时 makespan 最小;当 时,不妨先丢掉 job , 那么剩下的 job 按照前面所说的情况,每台机器都会处理其中两件,根据 LPT 流程,必然是第 大的 job 与第 的 job 在一台机器上处理,任意调换两个 job 都会使两台机器的 makespan 增大,因此此时必然是最优解,最后将 给最早完工的机器处理必然仍然是最优解。得证。
由上述证明过程,可以直接得到以下 Lemma.
Lemma 2.8
For any input to the problem of minimizing the makespan on identical parallel machines for which the processing requirement of each job is more than one-third the optimal makespan, the longest processing time rule computes an optimal schedule.
The traveling salesman problem
给定城市集合 和 的对称矩阵 表示从城市 到城市 的旅行花费. 我们约定没有自边, 且 cost 都 . 要求找到一个包含所有结点且仅包含一次的环, 使得环的路径花费之和最小.
如果将输入看作一个带权无向完全图, 则 feasible solution (即 tour) 由图中的 Hamiltonian cycle 构成.
decide 给定的无向图是否存在 Hamiltonian cycle 是 NP-complete 的, 能解决上述 TSP 问题的 approx alg 也能用来解决 Hamiltonian cycle 问题: 给定无向图 , 构造对应 TSP 的图, 对于每个二元组 , 若 , 则令 , 否则令 . 如果 存在 Hamiltonian cycle, 那么就会有一个 cost 为 的 tour, 否则 tour 的 cost 至少为 . 若我们有一个 2-approximation alg for the TSP, 如果它计算的 tour 至多为 , 就说明 中存在一条 Hamiltonian cycle, 否则不存在.
Theorem 2.9
For any , there does not exist an -approximation algorithm for the traveling salesman problem on cities, provided . In fact, the existence of an -approximation algorithm for the TSP would similarly imply that .
如果给边权加上 triangle inequality 的限制, 就可以避免上述转化, 从而可以对 TSP 进行求解, 此时的 TSP 被称为 metric TSP.
解决 metric TSP 的一个简单的 greedy heuristic 是: 先找到距离最近的两个城市 , 令目前的 tour 为 ; 之后不断迭代, 记 为当前 tour 包含的城市集合, 每轮找到一对城市 其中 且 最小, 将 加入 , 设 为 在当前 tour 中下一个到达的城市, 将 tour 改为 .
这个算法被称为 nearest addition algorithm, 它的过程与求解 MST 的 Prim 算法几乎一致, 我们借助 TSP 的最优解 MST 的边权和来分析 nearest addition algorithm.
Lemma 2.10
For any input to the traveling salesman problem, the cost of the optimal tour is at least the cost of the minimum spanning tree on the same input.
这个证明很简单, 将 optimal tour 任意去掉一条边便会得到一个特殊的 spanning tree, 并且这个 spanning tree 的 cost optimal tour 的 cost, 又由于 MST 的 cost 任意 spanning tree 的 cost, 因此引理成立.
Theorem 2.11
The nearest addition algorithm for the metric traveling salesman problem is a 2-approximation algorithm.
Proof
TODO
事实上, 有了 MST 这个桥梁后我们可以从另一个角度看待上述算法, 在这个角度下可以进一步优化. 首先需要知道一点: Eulerian graph 可以通过 shortcutting 得到一个 Hamiltonian cycle. 具体到本题, 假设我们已经计算出 的 MST, 然后将每条边 copy 一份, 此时每个点度数必然是偶数, 也就存在 Eulerian traversal, 并且新的 graph 的 cost . 令一个 Eulerian traversal 为 , 将对应的 path 罗列出来, 去除重复的结点仅保留它的第一次出现, 这样一来我们就得到了 的一个 tour.
接着我们 bound 这个 tour 的长度: 设 是 tour 中相邻的两个结点, 我们从 traversal 中去除了已经出现过了的结点 , 根据 triangle inequality, , 因此 tour cost traversal cost . 这个算法也被称为 double-tree algorithm.
Theorem 2.12
The double-tree algorithm for the metric traveling salesman problem is a 2-approximation algorithm.
"跳过"已经访问过的结点并利用未经"跳过"的原图的边权和来 bound 新得到的 tour 的 cost 的技术有时也被称为 shortcutting.
在 double-tree alg 将 MST 转化为 Eulerian 的过程可以进一步优化. 在 MST 中, 显然所有结点的度数之和为偶数, 对于度数本来就是偶数的结点可以不做修改, 考虑度数为奇数的结点集合 . 为了不动偶度数结点的连边, 我们只对 内部的连边作修改. 要保证图的连通性, 我们必然加边而不是减边, 要使加边的边权和尽可能小, 加的边数自然要尽可能小, 我们希望给每个结点仅加一条边, 此时问题转化为了求解 的 perfect matching. 给定一个完全带权图, 我们能在 polynomial time 找到权值最小的 perfect matching. 因此我们新加的边即为 的边权和最小的 perfect matching 的边, 这样 MST 便成为了 Eulerian graph, 接着我们按照 double-tree alg 后面的步骤走便可得到 的一个 tour. 这个算法被称为 Christofides’ algorithm.
Theorem 2.13
Christofides’ algorithm for the metric traveling salesman problem is a - approximation algorithm.
Proof
TODO
目前还没有找到比这个更优的 metric TSP 算法, 不过根据下面的定理, 也许还有更优一点的算法有待发现.
Theorem 2.14
Unless , for any constant , no -approximation algorithm for the metric TSP exists.
Maximizing float in bank accounts
float 指的是使用支票付款到银行将账户中这笔钱抽取出来的时间间距, maximizing float problem 指的是:
我们希望开不超过 个银行账户来最大化 float, 记 为可能开账户的银行集合, 为需要支付的 payees 的集合. 令 表示用在银行 的账户付款给 的 float 值. 我们希望找到 , 使得 最大. 我们定义 为选择 得到的这个 objective function 的值.
一个 natural greedy alg 是: 从 开始, 每次选择能使 的银行 将其加入 直到 .
 image.png
image.png
这个贪心看上去好像很对, 可惜的是 objective function 是 convex function 而不是 linear function, 局部最优并不等同于全局最优, 因而它只能是近似算法. 不过它的性能很优秀, 接下来我们证明它是 -approximation 的.
在证明之前, 我们首先提出一个 Lemma, 约定 为 最小的 optimal solution, 它满足 .
Lemma 2.15
Let be the set of banks at the start of some iteration of Algorithm 2.2, and let be the bank chosen in the iteration. Then
这个 Lemma 的 intuition 在于: 中每一个银行 , 都会在 中至少对应一个 payee 使得 , 否则 对 没有贡献, 没有必要将 加入 凑数, 由于 , 因此必然存在 使得 的贡献 . 显然加入的第一个银行 必然满足 , 直觉上来说, 必然还会存在银行满足贡献 中还为被分配出去的部分的 , 同样地也可以得出 的结论.
Theorem 2.16
Algorithm 2.2 gives a -approximation algorithm for the float maximization problem.
令 表示第 轮迭代后的结果, 于是 . 令 , 对任意 , 代入 Lemma 2.15 有 , 不断对 应用这个不等式可以得到
接下来我们证明 Lemma 2.15. Lemma 2.15 的证明又依赖于下述 Lemma:
Lemma 2.17
For the objective function , for any and any ,
这个 Lemma 的正确性很显然, formal proof 也比较简单, 这里不再赘述.
Submodularity
Lemma 2.17 反映的 value function 所具有的性质称为 submodularity, 它的主要含义是加入一个新元素能产生的 marginal value 会随着 set 的元素数量增加而减少, 这个性质在很多 algorithmic settings 中都起到了重要作用.
设 以及 , 由 且 , 显然 , 于是我们有
根据算法流程, 必然有 , 因此
类似的拥有以集合 来表示的 objective function , 同时满足 是 monotone 和 submodularity 的问题中都可以借鉴上述 greedy approx alg 以及它的分析.
Finding minimum-degree spanning trees
给定图 , 我们希望找到 的一个最小生成树 使得 中度数最大的结点的度数最小.
对于 的图 , 它的答案最小只能是 , 若确实是 就说明 存在一条 Hamiltonian path, 而决定图 中是否存在一条 Hamiltonian path 的问题是 NP-hard 的, 可见 minimum spanning tree problem 也是 NP-hard.
Theorem 2.18
It is NP-complete to decide whether or not a given graph has a minimum-degree spanning tree of maximum degree two.
对于图 , 设 为最优解得到的 MST, 为 中的 maximum degree. 下面给出一个能在 polynomial time 找到 maximum degree 不超过 的 local search algorithm.
该 local search algorithm 的基本设置如下: 从任意 MST 开始, 记 为 的 maximum degree, 为 在 中的 degree, 为了方便, 记 . local move 为选择一个结点 , 然后尝试遍历 添加一条不属于 的边 得到环 使得 位于 上并且满足 , 然后删除 上与 相连的一条边从而将 减少 1, 和 增加 1.
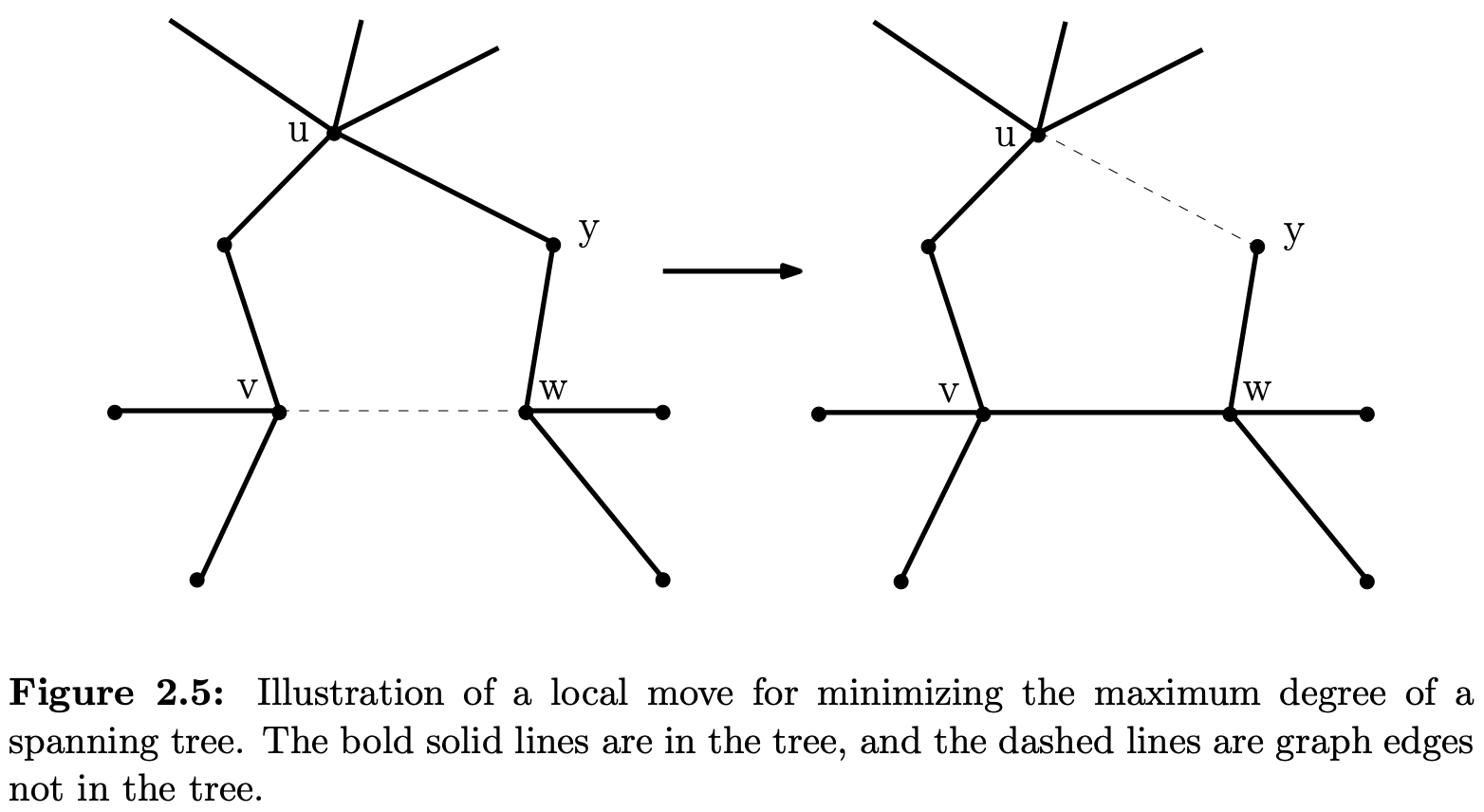
local search algorithm 会用上述 local move 不断减少某些结点的 degree 直到无法进行下一步 local move. 具体而言, 由于 degree 等于 的结点度数的减少可能依赖于一些其他结点度数的减少, 因此不仅要对具有 maximum degree 尝试 local move, 其他结点也要尝试; 为了算法能在 polynomial time 终止, 只对 degree 相对大的结点尝试 local move, 此处设置对 degree 位于 到 区间的结点尝试 local move. 当算法无法对目标结点进行 local move 时即终止, 此时我们称它找到了一个 locally optimal tree.
下面证明上述 local search algorithm 找到的 locally optimal tree 的 maximum degree 不会超过 .
Theorem 2.19
Let be a locally optimal tree. Then , where .
先对 的 lower bound 进行估计. 考虑下述情况, 对 MST 删去 条边, 则它会被分为 个 components, 此时存在一些结点, 设其集合为 , 将任意两个 component 相连都会用到与这些结点相连的边, 那么将这 个 components 相连得到新的 MST 平均会增加的 degree 为 , 显然 必然可以通过删边再加边得到, 因此必然有 .
接下来在 上寻找这样的 与 . 记 为 的点集, 考虑 local search algorithm 的终止态, 即 中不存在可以进行 local move 的结点. 那么对于任意 , 将 中与 中结点相邻的边删去, 删去的边数至少为 , 其中 为 内部最多可能的边数 (形成环的边数 - 1), 根据 local move 的描述, 不存在与 degree 的结点相连的边能连接任意两个被分开的 component, 从而 对应此时的 , 于是有 .
然后我们对 与 之间的大小关系进行估计. 由于满足条件的 可以任取, 因此不妨直接找到一个满足 的 . 考虑是否能找到这样的 . 若所有满足 都有 , 那么就会有 , 矛盾 (个人猜测 的值也是这么设置来的🤔), 从而必然能找到 满足 . 此时有
Theorem 2.20
The algorithm finds a locally optimal tree in polynomial time.
本题使用 potential function 进行证明. 对于树 , 定义它的 potential function 为 . 显然有 , Hamiltonian path 的 potential 为 , 因此 .
考虑 local move 对 potential 的影响. 假设一次 local move 将 从 减小到了 , potential 的减少值则为 , 而对应 degree 增加的结点 和 使 potential 增加的值不会超过 , 从而单次 local move 导致 potential 减少的值至少为 . 注意到每次 local move 的对象必然满足 , 而我们又有对 的估计:
因此整体的 potential 减少值至少为
即经过一次 local move 后得到的新 MST 有 . 而若一开始的 , 那么经过至多 次 local move, 会减小到 :
Note
potential function 能表示算法当前的 state, 而我们可以根据实际的 problem 给出 potential function 的 upper bound 以及 lower bound, 然后就可以借每次 move 后 function 取值变化来对可能的 move 数目进行估计.
potential function 的相性与 local search 很合得来, 也许是对 local search 分析的一个万金油方法? 它的思想也很有意思, 有种开启上帝视角的感觉, 相信在别的地方也很有用.
有了上述分析, 不难得出下述推论:
Corollary 2.21
The local search algorithm runs in polynomial time and results in a spanning tree such that .
Edge Coloring
本节介绍同时具有 greedy algorithm 和 local search algorithm 的特点的一个算法: 它尝试做出 greedy decision, 当无法进行下一步时就 make local changes 直到可以继续.
这个算法是用来找到一张图的 edge coloring 的. 若一张无向图中所有边可以被恰好 个颜色之一染色并且满足不存在两个颜色相同的边有公共点, 我们就称这个图是 -edge-colorable.
对于给定的 -edge-colorable 的图, 我们希望 越小越好. 令 表示图中的 maximum degree, 显然有 , 并且不是所有的图都能满足 , 例如 Petersen graph:
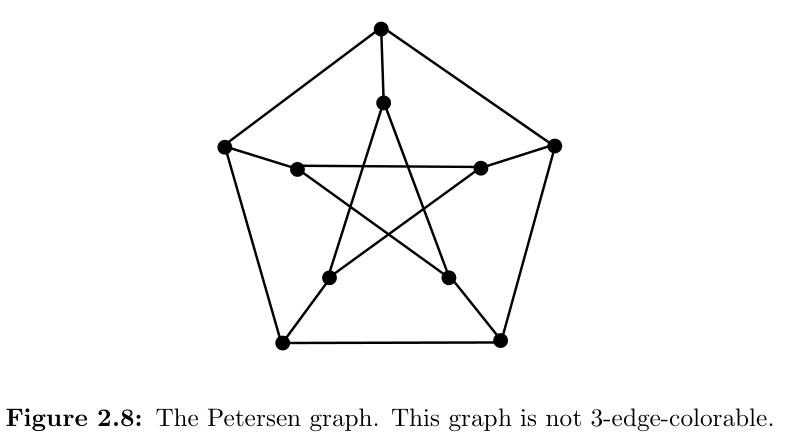
Theorem 2.22
For graphs with , it is NP-complete to decide whether the graph is 3-edge-colorable or not.
这里我们给出的算法能在 polynomial time 找出任意图的 -edge-coloring, 它从完全未被染色的图开始, 每一轮迭代从一个未被染色的边 开始, 然后建立 fan sequence, 将 shifting color 作为 local move 来允许贪心能进行下去.

Theorem 2.23
There is a polynomial-time algorithm to find a -edge-coloring of a graph.
对于算法能成功找到一个 -edge-coloring, 只需证明算法每一次迭代都能成功染色一条未被染色的边即可. 在单轮迭代中, 算法首先寻找一条未被染色的边 , 尝试将其染色:
- 若存在 color 使得 和 都不存在邻边被染上过 (称之为 lack ), 则直接染色 ;
- 若不存在, 则考虑 shifting color: 随机选择颜色 使得 lacks 但是 并不 lack, 接着将 uncolored edge 切换到颜色为 的 , 同样尝试寻找 都 lack 的颜色, 若找到则直接染上该颜色, 将 给 , 否则继续上述流程, 维护当前的边序列 和对应的颜色序列 .
- 当找到 是 和 都 lack 的颜色时即终止, 然后分别将边序列中的边染上颜色序列中的颜色即可, 相当于完成了一系列的 color shift 并成功将最初的 uncolored edge 染色.
- 另一种情况是存在 使得 , 此时显然无法继续维护边序列与颜色序列, 考虑如何做 local change 来得以继续: 显然需要给 引入新的 color , 根据算法描述, 与 都并不 lack , 而 lack . 不妨在只由用 与 染色的边集得到的 的子图 上考虑问题. 不难发现, 只会由一些简单路径及大小为偶数的环组成, 由于 都只拥有 中的一种颜色, 因此他们都只能是简单路径的端点之一, 一条简单路径只有 2 个端点, 因此三个结点至多有两个位于同一条简单路径上, 不妨设其为 , 我们将这条路径上的颜色进行调换, 这样一来 和 都 lack 而不 lack , lack 而不 lack , 然后用 染色 , 于是 这部分 fan sequence 依然可以运用上一种情况的 color shifting 将未染色的边 染色.
- 从而算法的每一轮迭代都能成功染色一条 uncolored edge, 至多 次迭代可以得到一个 -edge-coloring.
迭代次数是 的, 每一轮迭代内部也是 polynomial-time 的, 因此算法显然是 polynomial-time algorithm.
Author: f1a3h
Permalink: https://blog.rbkou.me/Study-Notes/Approx-Alg/tdaa-ch2/
文章默认使用 CC BY-NC-SA 4.0 协议进行许可,使用时请注意遵守协议。
Comments